دوره 15، شماره 3 - ( پاییز 1399 )
جلد 15 شماره 3 صفحات 285-278 |
برگشت به فهرست نسخه ها
Download citation:
BibTeX | RIS | EndNote | Medlars | ProCite | Reference Manager | RefWorks
Send citation to:



BibTeX | RIS | EndNote | Medlars | ProCite | Reference Manager | RefWorks
Send citation to:
Bakhshi A, Bakhshi E. Introducing a Formula for Obtaining the Total Deviation Index in Aging Studies. Salmand: Iranian Journal of Ageing 2020; 15 (3) :278-285
URL: http://salmandj.uswr.ac.ir/article-1-1881-fa.html
URL: http://salmandj.uswr.ac.ir/article-1-1881-fa.html
بخشی اندیشه، بخشی عنایتاله. کاربرد شاخص انحراف کل در مطالعات سالمندی. سالمند: مجله سالمندی ایران. 1399; 15 (3) :278-285
1- دانشکده محاسبات، مهندسی و علوم فیزیک، دانشگاه غرب اسکاتلند، گلاسگو.
2- گروه آمار زیستی و اپیدمیولوژی، دانشگاه علوم بهزیستی و توانبخشی، تهران، ایران. ،bakhshi@razi.tums.ac.ir
2- گروه آمار زیستی و اپیدمیولوژی، دانشگاه علوم بهزیستی و توانبخشی، تهران، ایران. ،
متن کامل [PDF 3079 kb]
(1888 دریافت)
| چکیده (HTML) (4191 مشاهده)
References
1.Lin LI. Total deviation index for measuring individual agreement with applications in laboratory performance and bioequivalence. Statistics in Medicine. 2000; 19(2):255-70. [DOI:10.1002/(sici)1097-0258(20000130)19:2<255::aid-sim293>3.0.co;2-8] [PMID]
2.McHorney CA, Ware Jr JE, Rachel Lu JF, Sherbourne CD. The MOS 36-item Short-Form Health Survey (SF-36): III. Tests of data quality, scaling assumptions, and reliability across diverse patient groups. Medical Care. 1994; 32(1):40-66. [DOI:10.1097/00005650-199401000-00004] [PMID]
3.Pan Y, Barnhart HX. Methods for assessing the reliability of quality of life based on SF-36. Statistics in Medicine. 2016; 35(30):5656-65. [DOI:10.1002/sim.7085] [PMID]
4.Montazeri A, Goshtasebi A, Vahdaninia M, Gandek B. The Short Form Health Survey (SF-36): Translation and validation study of the Iranian version. Quality of Life Research. 2005; 14(3):875-82. [DOI:10.1007/s11136-004-1014-5] [PMID]
5.Lin L, Pan Y, Hedayat AS, Barnhart HX, Haber M. A simulation study of nonparametric total deviation index as a measure of agreement based on quantile regression. Journal of Biopharmaceutical Statistics. 2016; 26(5):937-50. [DOI:10.1080/10543406.2015.1094812] [PMID]
متن کامل: (1945 مشاهده)
مقدمه
از آنجا که تحقیق بر نمونههای سالمندان و ثبت دادههای مربوطه نیازمند دقت بیشتری است، محاسبه خطای اندازهگیری از اهمیت زیادی برخوردار است. پرسشنامه به عنوان ابزار اندازهگیری در بسیاری از مطالعات استفاده میشود. هر پرسشنامه باید از روایی و پایایی مطلوبی برخوردار باشد تا بتواند دادههای قابل قبولی را جمعآوری نماید. خطای اندازهگیری در جمعآوری هر نوع دادهای، مورد توجه است. به طور کلی از ضریب همبستگی درونردهای (ICC) (معادل ریاضی آلفای کرونباخ) به عنوان ضریب پایایی پرسشنامه استفاده میشود.
به زبان سادهتر این ضریب، پایایی درونی را میسنجد و نشان میدهد که چقدر این آیتمها به عنوان یک مجموعه با هم رابطه دارند. در عمل با تکرار سنجش از افراد ضریب ICC به دست میآید که هر چقدر این ضریب به یک نزدیکتر باشد، نشاندهنده پایایی بیشتر است. اگر چه معمولاً حداقل مقدار ICC جهت گزارش پایایی ابزارها ارائه میشود، ولی شاخص ICC نمیتواند مشخص کند که چقدر از اختلاف در زیرمقیاسها مربوط به خطای اندازهگیری است. به طور واضحتر نه آلفای کرونباخ و نه ICC نمیتوانند مشخص کنند که چقدر از تغییرات (اختلافات) در زیرمقیاسها میتواند به علت خطای اندازهگیری باشد. لین و همکاران از شاخص انحراف کل (TDI) برای ارزیابی انحرافات بین جفت مشاهدات بهره بردند [1 ،2]. پان و همکاران نیز با تغییراتی در این شاخص، از آن جهت محاسبه خطای اندازهگیری استفاده کردند [3].
اندازهگیری «کیفیت زندگی» به عنوان یکی از شاخصهای مهم در سنجش سلامت افراد یک جامعه، به خصوص سالمندان توسط پژوهشگران حوزه سلامت از اهمیت خاصی برخوردار است. پرسشنامه SF-36 به عنوان ابزاری برای سنجش کیفیت زندگی استفاده میشود. این پرسشنامه دارای 36 آیتم است که یک آیتم تغییر در وضعیت سلامت فرد را در یک سال گذشته مد نظر دارد. مابقی 35 آیتم در محاسبه 8 خردهمقیاس عملکرد جسمی، کارکرد جسمی، دردهای جسمی، سلامت عمومی، سرزندگی (نشاط)، عملکرد اجتماعی، کارکرد عاطفی و سلامت روان استفاده میشوند. همچنین با استفاده از زیرمقیاسهای فوق، دو سنجش خلاصه به نامهای سلامت جسمی و سلامت روانی نیز محاسبه میشوند.
نمرات پرسشنامه معمولاً به مقیاس صفر تا صد تبدیل شده که نمره بیشتر نشاندهنده کیفیت زندگی بالاتر است. بیشتر مطالعات، پایایی بین 0/72 تا 0/95 را به دست آوردهاند و نشان دادهاند که حداقل پایایی این پرسشنامه 0/70 است [2]. پرسشنامه فوق توسط منتظری و همکاران به فارسی ترجمه شده و روایی و پایایی آن با حجم نمونه مناسب سنجیده شده است (به جز زیرآیتم نشاط که مقدار آلفای کرونباخی برابر با 0/65 را نشان داد، برای بقیه زیرآیتمها عددی بین 0/77 تا 0/99 حاصل شد) [4]. مطالعه حاضر با هدف معرفی فرمولی ساده جهت محاسبه TDI، تفسیر آن و ترغیب پژوهشگران در استفاده از این شاخص به عنوان ابزاری مناسب جهت تعیین پایایی در مطالعات روانسنجی طرحریزی شد.
روش مطالعه
مروری بر ICC
با توجه به مطالعه پان و همکاران [3]، فرض کنید که Sij نشاندهنده امتیازی است که به فرد iام برای آیتم jام نسبت داده شده است. این امتیاز را میتوان طبق فرمول شماره 1 به سه مؤلفه تقسیم کرد:
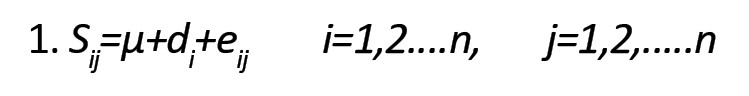
در این رابطه،µ نشاندهنده میانگین جامعه، diمعرف اختلاف امتیاز فرد iام از میانگین جامعه است که فرض میشود دارای توزیع نرمال با میانگین صفر و واریانس σ2d (برای تمام افراد) است. eij نشاندهنده خطای اندازهگیری که فرض میشود از توزیع نرمال با میانگین صفر و واریانس σ2e (برای تمام افراد و آیتمها) تبعیت میکند. همچنین مدل فرض میکند که eijها از هم مستقل و از diها نیز مستقل هستند. با این فرضها میتوان گفت که برای فرد iام مقادیر Sij برای آیتمها به عنوان همتایی برای اندازه واقعی µ+di است. بنابراین، میتوان بحث پایایی را به عنوان تکرارپذیری در نظر گرفت. گر چه امتیاز زیرمقیاسهای پرسشنامه SF-36 به عنوان متوسط امتیازات در نظر گرفته میشود، ولی میتوان پایایی را برای هر آیتم نیز در نظر گرفت. به عبارتی پایایی را هم برای امتیاز هر آیتم؛ یعنیSij و هم برای متوسط امتیازات؛ یعنی میتوان مد نظر قرار داد.
یکی از ملاکهای تعیین پایایی ICC است. اگر چه نسخههای مختلفی ازICC ارائه شده است، ولی نسخه اصلی آن که جهت پایایی یک آیتم استفاده میشود را با توجه به مدل شماره (1) میتوان به صورت نسبت واریانس مقدار واقعی به واریانس مشاهده شده به صورت زیر توسط فرمول شماره (2) تعریف کرد:
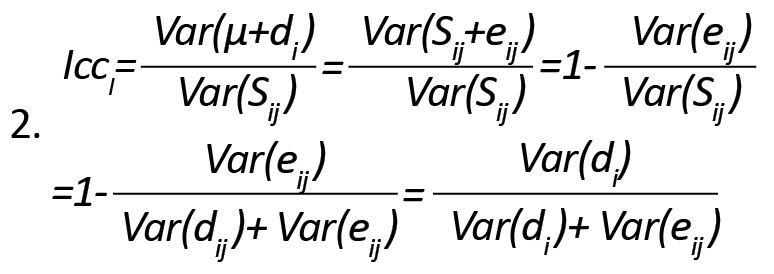
اگر بخواهیم پایایی را برای متوسط امتیازات از k آیتم محاسبه کنیم، ابتدا با توجه به مدل رابطه (1) متوسط امتیازات را به صورت زیر محاسبه می کنیم (فرمول شماره 3):
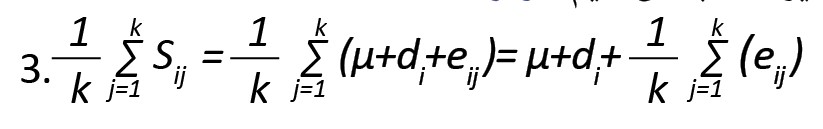
سپس ICC برای متوسط امتیازات حاصل از k آیتم به صورت زیر توسط رابطه شماره (4) محاسبه میشود:
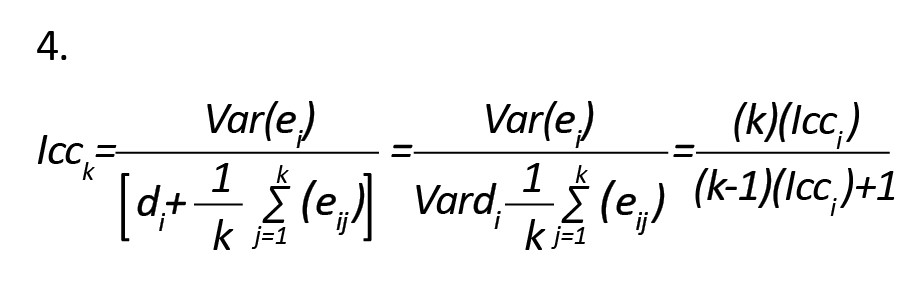
واضح است که با افزایش تعداد آیتمها پایایی افزایش مییابد.
شاخص انحراف کل
اگر چه استفاده از ICC در بسیاری از آزمونها رایج است، باید توجه داشت که این شاخص فاقد واحد اندازهگیری است. مثلاً وقتی دو متوسط امتیاز روی یک فرد داشته باشیم، مشخص نمیکند که چقدر از این اختلاف مربوط به خطای اندازهگیری است. از لحاظ مفهومی شاخص انحراف کل (Total Deviation Index(TDI)) مقدار خطای اندازهگیری را بر حسب واحد اندازهگیری بیان میکند.
TDI در ابتدا به منظور محاسبه توافق بین دو ارزیاب یا دو روش ارزیابی ارائه شد و سپس کاربرد بیشتری از آن مورد توجه قرار گرفت. TDI را شبیه ICC میتوان برای یک آیتم و یا متوسط امتیازات چند آیتم نیز محاسبه کرد. اگر دو امتیاز مختلف در دو بار اندازهگیری یک آیتم را در نظر بگیرید، TDI مشخص میکند که با احتمال مشخصی (مثلاً 95%) اختلاف این دو امتیاز از چه مقداری کمتر است؟ به عبارتی با احتمال مثلاً 95% ماکزیمم خطای اندازهگیری را بر حسب واحد اندازهگیری بیان میکند. اگر فرض کنید که امتیاز هر آیتم در مدل شماره (1) دارای توزیع نرمال باشد، در این صورت اختلاف هر دو امتیاز نیز دارای توزیع نرمال با میانگین صفر و واریانس یکسان هستند و با محاسبات ریاضی، میتوان TDI برای یک آیتم را طبق رابطه شماره (5) و به صورت زیر به دست آورد [3]:
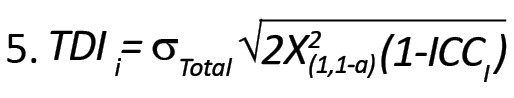
که در آن، σTotal نشاندهنده انحراف معیار کل و صدک توزیع کااسکور است که از جدول مربوطه به دست میآید.
دقت کنید که در بسیاری از پرسشنامهها، متوسط تعدادی از آیتمها را به عنوان زیرمقیاس محاسبه میکنند. با فرض نرمال بودن امتیاز هر آیتم در مدل شماره (1)، اختلاف هر دو متوسط امتیازات، دارای توزیع نرمال با میانگین صفر و واریانس یکسان هستند. در این صورت میتوان TDI برای زیر مقیاسها را نیز به صورت رابطه شماره (6) محاسبه کرد:
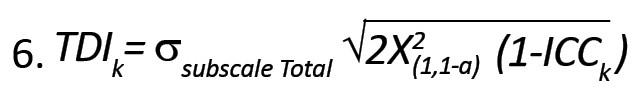
که در آن،σsubscale Total نشاندهنده انحراف معیار زیرمقیاسها است.
حالات خاص: دقت کنید که برای استفاده از فرمول شماره (5) باید صدکهای توزیع کااسکور را از جدول مربوطه به دست آورده و در فرمول قرار دهید. در حالت خاص برای احتمالات 95، 90 و 80 درصد فرمول به صورت سادهتر در رابطهی شماره 7 قابل استفاده است:
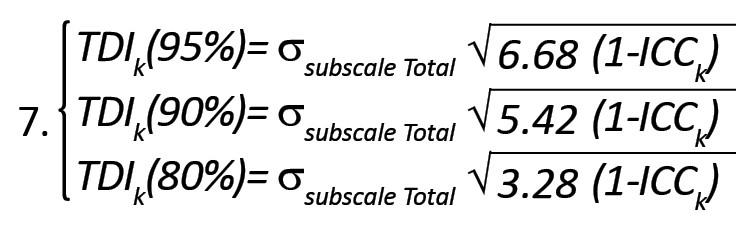
مثال کاربردی
پس از انتخاب 105 سالمند از جامعه سالمندان در سطح شهر تهران (به صورت دسترس در پاییز سال 1398)، پرسشنامه 36-SF برای آنها تکمیل شد. پس از دو هفته مجدداً پرسشنامه تکمیل شد. در تجزیه و تحلیل مقدار شاخص ICC و همچنین انحراف معیار زیرمقیاسها به دست آمدند. در نهایت TDI برای زیرمقیاسها به صورت جداگانه محاسبه شدند. جدول شماره 1 این مقادیر را نشان میدهد.
.jpg)
دقت کنید که مقادیر TDI طبق فرمول خیلی ساده محاسبه میشود. به عنوان مثال، مقدار TDI برای زیرمقیاس «عملکرد جسمی» به صورت زیر محاسبه میشود (فرمول شماره 8):
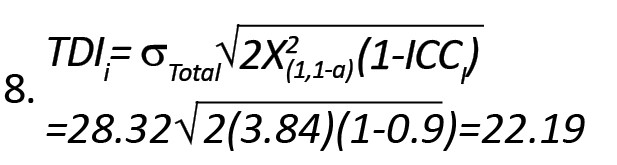
نشان میدهد که با احتمال 95 درصد، حداکثر 22 واحد (از صد واحد) خطای اندازهگیری است. سایر مقادیر TDI نیز به همین صورت به دست میآیند.
دقت کنید که مقادیر TDI برای زیرمقیاسها از حدود 22 تا 34 واحد تغییر میکند که کمترین خطا مربوط به زیرمقیاس «عملکرد جسمی» و بیشترین خطا مربوط به زیرمقیاس «مشکلات روحی» است. ذکر این نکته قابل توجه است که مقادیر ICC و TDI لزوماً تغییرات یکسانی ندارند. مثلاً هر دو شاخص در زیرمقیاس «مشکلات جسمی» بیشتر از زیرمقیاس «سلامت روان» هستند. در حالی که اگر زیرمقیاس «مشکل جسمی» را با زیر مقیاس «سلامت روان» مقایسه کنید، مقدار ICC در «مشکلات جسمی» کمتر از «عملکرد جسمی» است، ولی مقدار TDI برای آن بیشتر است. به منظور آنالیز بیشتر، معنیدار بودن ضریب همبستگی اسپیرمن بین ICC و TDI آزمون شد که نتیجه نشان داد آزمون همبستگی معنیدار نیست (P=0/551).
بحث
در این مطالعه با استفاده از شاخصی به نام TDI حداکثر خطای اندازهگیری پرسشنامه 36-SF با احتمال 95 درصد به دست آمد. تفسیر TDI خیلی ساده است و حداکثر خطای اندازهگیری را با احتمال بیان میکند. اگر چه محاسبات با احتمال 95 درصد انجام شدند، میتوان با هر احتمال دیگری TDI را به دست آورد. همچنین نشان داده شد که مقادیر TDI لزوماً با مقادیر ICC در یک راستا نیستند؛ یعنی اگر مقدار ICC زیاد باشد لزومی ندارد که مقدار TDI کم شود و برعکس. نتایج به دست آمده از این پژوهش با برخی مطالعات همسو هستند [3].
اگر چه در مثال استفاده شده از نمرهدهی صفر تا 100 برای پرسشنامه 36-SF استفاده شد و همه زیرمقیاسها نیز از همین نوع امتیازدهی استفاده کردند، میتوان TDI را در هر حالتی که هر نوع امتیازدهی دیگری (مثل امتیاز خام پرسشنامه) به کار رفته باشد نیز به دست آورده و به صورت مشابه تفسیر کرد. اگر چه میانگینگیری از آیتمها باعث افزایش پایایی میشود، افزایش تعداد آیتمها نیز در افزایش پایایی مؤثر است.
فرمول محاسبه TDI در اینجا با فرض نرمال بودن توزیع آیتمها در هر زیرمقیاس (و یا متوسط امتیازات هر زیرمقیاس) به دست آمد. اگر فرض نرمال بودن نقض شود، میتوان روشهای ناپارامتری را به کار برد. یکی از این روشها استفاده از رگرسیون چندکی است [5]. البته باید توجه داشت که اگر امتیاز هر مقیاس جداگانه مورد نظر باشد، بعد از تکرار اندازهگیری و محاسبه ICC روش رگرسیون چندکی به راحتی به کار برده میشود. ولی اگر میانگین آیتمها در هر زیرمقیاس مورد نظر باشد، محاسبه TDI به راحتی صورت نمیگیرد و مشکلاتی در استفاده از این روش وجود دارد.
نتیجهگیری نهایی
از آنجا که شاخص ICC نمیتواند مشخص کند که چقدر از اختلاف در زیرمقیاسها مربوط به خطای اندازهگیری است و همچنین با توجه به تفسیر ساده شاخص انحراف کل، پیشنهاد میشود که پژوهشگران شاخص انحراف کل را در مطالعات پایایی گزارش نمایند.
ملاحظات اخلاقی
پیروی از اصول اخلاق پژوهش
این پژوهش بر گرفته از یک طرح تحقیقاتی است که پروپوزال آن در کمیته اخلاق دانشگاه علوم بهزیستی و توانبخشی مورد تأیید قرار گرفته است (کد: IR.USWR.REC.13960379).
حامی مالی
این پژوهش هیچگونه کمک مالی از سازمانیهای دولتی، خصوصی و غیرانتفاعی دریافت نکرده است.
مشارکت نویسندگان
هر دو نویسنده در آمادهسازی این مقاله مشارکت داشتهاند.
تعارض منافع
نویسندگان اظهار میدارند که این پژوهش هیچ تعارض منافعی ندارد.
از آنجا که تحقیق بر نمونههای سالمندان و ثبت دادههای مربوطه نیازمند دقت بیشتری است، محاسبه خطای اندازهگیری از اهمیت زیادی برخوردار است. پرسشنامه به عنوان ابزار اندازهگیری در بسیاری از مطالعات استفاده میشود. هر پرسشنامه باید از روایی و پایایی مطلوبی برخوردار باشد تا بتواند دادههای قابل قبولی را جمعآوری نماید. خطای اندازهگیری در جمعآوری هر نوع دادهای، مورد توجه است. به طور کلی از ضریب همبستگی درونردهای (ICC) (معادل ریاضی آلفای کرونباخ) به عنوان ضریب پایایی پرسشنامه استفاده میشود.
به زبان سادهتر این ضریب، پایایی درونی را میسنجد و نشان میدهد که چقدر این آیتمها به عنوان یک مجموعه با هم رابطه دارند. در عمل با تکرار سنجش از افراد ضریب ICC به دست میآید که هر چقدر این ضریب به یک نزدیکتر باشد، نشاندهنده پایایی بیشتر است. اگر چه معمولاً حداقل مقدار ICC جهت گزارش پایایی ابزارها ارائه میشود، ولی شاخص ICC نمیتواند مشخص کند که چقدر از اختلاف در زیرمقیاسها مربوط به خطای اندازهگیری است. به طور واضحتر نه آلفای کرونباخ و نه ICC نمیتوانند مشخص کنند که چقدر از تغییرات (اختلافات) در زیرمقیاسها میتواند به علت خطای اندازهگیری باشد. لین و همکاران از شاخص انحراف کل (TDI) برای ارزیابی انحرافات بین جفت مشاهدات بهره بردند [1 ،2]. پان و همکاران نیز با تغییراتی در این شاخص، از آن جهت محاسبه خطای اندازهگیری استفاده کردند [3].
اندازهگیری «کیفیت زندگی» به عنوان یکی از شاخصهای مهم در سنجش سلامت افراد یک جامعه، به خصوص سالمندان توسط پژوهشگران حوزه سلامت از اهمیت خاصی برخوردار است. پرسشنامه SF-36 به عنوان ابزاری برای سنجش کیفیت زندگی استفاده میشود. این پرسشنامه دارای 36 آیتم است که یک آیتم تغییر در وضعیت سلامت فرد را در یک سال گذشته مد نظر دارد. مابقی 35 آیتم در محاسبه 8 خردهمقیاس عملکرد جسمی، کارکرد جسمی، دردهای جسمی، سلامت عمومی، سرزندگی (نشاط)، عملکرد اجتماعی، کارکرد عاطفی و سلامت روان استفاده میشوند. همچنین با استفاده از زیرمقیاسهای فوق، دو سنجش خلاصه به نامهای سلامت جسمی و سلامت روانی نیز محاسبه میشوند.
نمرات پرسشنامه معمولاً به مقیاس صفر تا صد تبدیل شده که نمره بیشتر نشاندهنده کیفیت زندگی بالاتر است. بیشتر مطالعات، پایایی بین 0/72 تا 0/95 را به دست آوردهاند و نشان دادهاند که حداقل پایایی این پرسشنامه 0/70 است [2]. پرسشنامه فوق توسط منتظری و همکاران به فارسی ترجمه شده و روایی و پایایی آن با حجم نمونه مناسب سنجیده شده است (به جز زیرآیتم نشاط که مقدار آلفای کرونباخی برابر با 0/65 را نشان داد، برای بقیه زیرآیتمها عددی بین 0/77 تا 0/99 حاصل شد) [4]. مطالعه حاضر با هدف معرفی فرمولی ساده جهت محاسبه TDI، تفسیر آن و ترغیب پژوهشگران در استفاده از این شاخص به عنوان ابزاری مناسب جهت تعیین پایایی در مطالعات روانسنجی طرحریزی شد.
روش مطالعه
مروری بر ICC
با توجه به مطالعه پان و همکاران [3]، فرض کنید که Sij نشاندهنده امتیازی است که به فرد iام برای آیتم jام نسبت داده شده است. این امتیاز را میتوان طبق فرمول شماره 1 به سه مؤلفه تقسیم کرد:
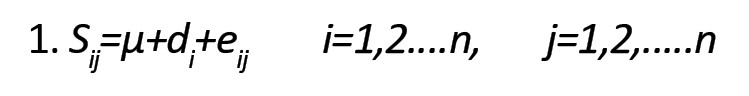
در این رابطه،µ نشاندهنده میانگین جامعه، diمعرف اختلاف امتیاز فرد iام از میانگین جامعه است که فرض میشود دارای توزیع نرمال با میانگین صفر و واریانس σ2d (برای تمام افراد) است. eij نشاندهنده خطای اندازهگیری که فرض میشود از توزیع نرمال با میانگین صفر و واریانس σ2e (برای تمام افراد و آیتمها) تبعیت میکند. همچنین مدل فرض میکند که eijها از هم مستقل و از diها نیز مستقل هستند. با این فرضها میتوان گفت که برای فرد iام مقادیر Sij برای آیتمها به عنوان همتایی برای اندازه واقعی µ+di است. بنابراین، میتوان بحث پایایی را به عنوان تکرارپذیری در نظر گرفت. گر چه امتیاز زیرمقیاسهای پرسشنامه SF-36 به عنوان متوسط امتیازات در نظر گرفته میشود، ولی میتوان پایایی را برای هر آیتم نیز در نظر گرفت. به عبارتی پایایی را هم برای امتیاز هر آیتم؛ یعنیSij و هم برای متوسط امتیازات؛ یعنی میتوان مد نظر قرار داد.
یکی از ملاکهای تعیین پایایی ICC است. اگر چه نسخههای مختلفی ازICC ارائه شده است، ولی نسخه اصلی آن که جهت پایایی یک آیتم استفاده میشود را با توجه به مدل شماره (1) میتوان به صورت نسبت واریانس مقدار واقعی به واریانس مشاهده شده به صورت زیر توسط فرمول شماره (2) تعریف کرد:
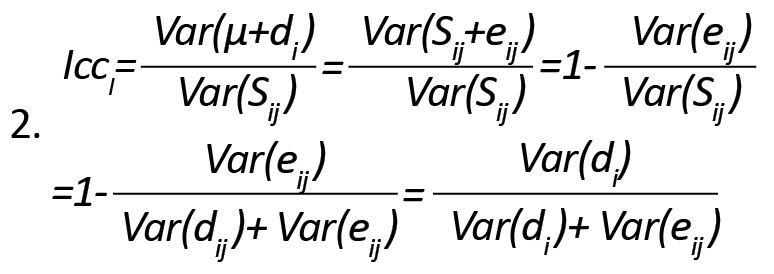
اگر بخواهیم پایایی را برای متوسط امتیازات از k آیتم محاسبه کنیم، ابتدا با توجه به مدل رابطه (1) متوسط امتیازات را به صورت زیر محاسبه می کنیم (فرمول شماره 3):
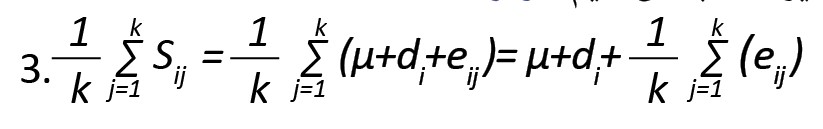
سپس ICC برای متوسط امتیازات حاصل از k آیتم به صورت زیر توسط رابطه شماره (4) محاسبه میشود:
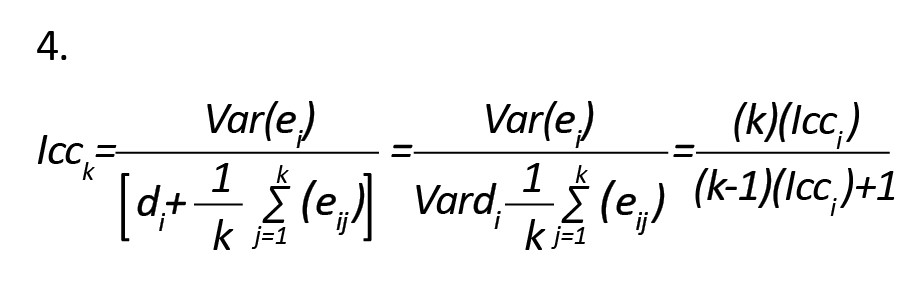
واضح است که با افزایش تعداد آیتمها پایایی افزایش مییابد.
شاخص انحراف کل
اگر چه استفاده از ICC در بسیاری از آزمونها رایج است، باید توجه داشت که این شاخص فاقد واحد اندازهگیری است. مثلاً وقتی دو متوسط امتیاز روی یک فرد داشته باشیم، مشخص نمیکند که چقدر از این اختلاف مربوط به خطای اندازهگیری است. از لحاظ مفهومی شاخص انحراف کل (Total Deviation Index(TDI)) مقدار خطای اندازهگیری را بر حسب واحد اندازهگیری بیان میکند.
TDI در ابتدا به منظور محاسبه توافق بین دو ارزیاب یا دو روش ارزیابی ارائه شد و سپس کاربرد بیشتری از آن مورد توجه قرار گرفت. TDI را شبیه ICC میتوان برای یک آیتم و یا متوسط امتیازات چند آیتم نیز محاسبه کرد. اگر دو امتیاز مختلف در دو بار اندازهگیری یک آیتم را در نظر بگیرید، TDI مشخص میکند که با احتمال مشخصی (مثلاً 95%) اختلاف این دو امتیاز از چه مقداری کمتر است؟ به عبارتی با احتمال مثلاً 95% ماکزیمم خطای اندازهگیری را بر حسب واحد اندازهگیری بیان میکند. اگر فرض کنید که امتیاز هر آیتم در مدل شماره (1) دارای توزیع نرمال باشد، در این صورت اختلاف هر دو امتیاز نیز دارای توزیع نرمال با میانگین صفر و واریانس یکسان هستند و با محاسبات ریاضی، میتوان TDI برای یک آیتم را طبق رابطه شماره (5) و به صورت زیر به دست آورد [3]:
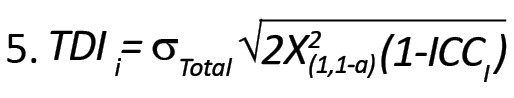
که در آن، σTotal نشاندهنده انحراف معیار کل و صدک توزیع کااسکور است که از جدول مربوطه به دست میآید.
دقت کنید که در بسیاری از پرسشنامهها، متوسط تعدادی از آیتمها را به عنوان زیرمقیاس محاسبه میکنند. با فرض نرمال بودن امتیاز هر آیتم در مدل شماره (1)، اختلاف هر دو متوسط امتیازات، دارای توزیع نرمال با میانگین صفر و واریانس یکسان هستند. در این صورت میتوان TDI برای زیر مقیاسها را نیز به صورت رابطه شماره (6) محاسبه کرد:
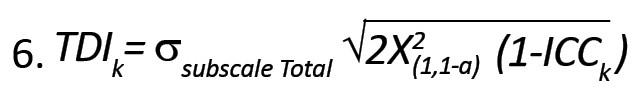
که در آن،σsubscale Total نشاندهنده انحراف معیار زیرمقیاسها است.
حالات خاص: دقت کنید که برای استفاده از فرمول شماره (5) باید صدکهای توزیع کااسکور را از جدول مربوطه به دست آورده و در فرمول قرار دهید. در حالت خاص برای احتمالات 95، 90 و 80 درصد فرمول به صورت سادهتر در رابطهی شماره 7 قابل استفاده است:
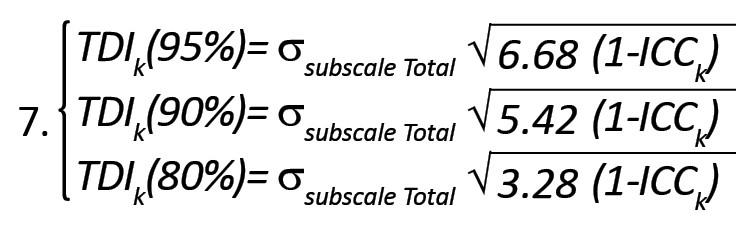
مثال کاربردی
پس از انتخاب 105 سالمند از جامعه سالمندان در سطح شهر تهران (به صورت دسترس در پاییز سال 1398)، پرسشنامه 36-SF برای آنها تکمیل شد. پس از دو هفته مجدداً پرسشنامه تکمیل شد. در تجزیه و تحلیل مقدار شاخص ICC و همچنین انحراف معیار زیرمقیاسها به دست آمدند. در نهایت TDI برای زیرمقیاسها به صورت جداگانه محاسبه شدند. جدول شماره 1 این مقادیر را نشان میدهد.
.jpg)
دقت کنید که مقادیر TDI طبق فرمول خیلی ساده محاسبه میشود. به عنوان مثال، مقدار TDI برای زیرمقیاس «عملکرد جسمی» به صورت زیر محاسبه میشود (فرمول شماره 8):
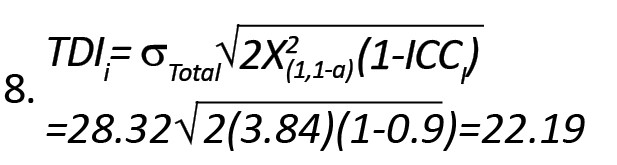
نشان میدهد که با احتمال 95 درصد، حداکثر 22 واحد (از صد واحد) خطای اندازهگیری است. سایر مقادیر TDI نیز به همین صورت به دست میآیند.
دقت کنید که مقادیر TDI برای زیرمقیاسها از حدود 22 تا 34 واحد تغییر میکند که کمترین خطا مربوط به زیرمقیاس «عملکرد جسمی» و بیشترین خطا مربوط به زیرمقیاس «مشکلات روحی» است. ذکر این نکته قابل توجه است که مقادیر ICC و TDI لزوماً تغییرات یکسانی ندارند. مثلاً هر دو شاخص در زیرمقیاس «مشکلات جسمی» بیشتر از زیرمقیاس «سلامت روان» هستند. در حالی که اگر زیرمقیاس «مشکل جسمی» را با زیر مقیاس «سلامت روان» مقایسه کنید، مقدار ICC در «مشکلات جسمی» کمتر از «عملکرد جسمی» است، ولی مقدار TDI برای آن بیشتر است. به منظور آنالیز بیشتر، معنیدار بودن ضریب همبستگی اسپیرمن بین ICC و TDI آزمون شد که نتیجه نشان داد آزمون همبستگی معنیدار نیست (P=0/551).
بحث
در این مطالعه با استفاده از شاخصی به نام TDI حداکثر خطای اندازهگیری پرسشنامه 36-SF با احتمال 95 درصد به دست آمد. تفسیر TDI خیلی ساده است و حداکثر خطای اندازهگیری را با احتمال بیان میکند. اگر چه محاسبات با احتمال 95 درصد انجام شدند، میتوان با هر احتمال دیگری TDI را به دست آورد. همچنین نشان داده شد که مقادیر TDI لزوماً با مقادیر ICC در یک راستا نیستند؛ یعنی اگر مقدار ICC زیاد باشد لزومی ندارد که مقدار TDI کم شود و برعکس. نتایج به دست آمده از این پژوهش با برخی مطالعات همسو هستند [3].
اگر چه در مثال استفاده شده از نمرهدهی صفر تا 100 برای پرسشنامه 36-SF استفاده شد و همه زیرمقیاسها نیز از همین نوع امتیازدهی استفاده کردند، میتوان TDI را در هر حالتی که هر نوع امتیازدهی دیگری (مثل امتیاز خام پرسشنامه) به کار رفته باشد نیز به دست آورده و به صورت مشابه تفسیر کرد. اگر چه میانگینگیری از آیتمها باعث افزایش پایایی میشود، افزایش تعداد آیتمها نیز در افزایش پایایی مؤثر است.
فرمول محاسبه TDI در اینجا با فرض نرمال بودن توزیع آیتمها در هر زیرمقیاس (و یا متوسط امتیازات هر زیرمقیاس) به دست آمد. اگر فرض نرمال بودن نقض شود، میتوان روشهای ناپارامتری را به کار برد. یکی از این روشها استفاده از رگرسیون چندکی است [5]. البته باید توجه داشت که اگر امتیاز هر مقیاس جداگانه مورد نظر باشد، بعد از تکرار اندازهگیری و محاسبه ICC روش رگرسیون چندکی به راحتی به کار برده میشود. ولی اگر میانگین آیتمها در هر زیرمقیاس مورد نظر باشد، محاسبه TDI به راحتی صورت نمیگیرد و مشکلاتی در استفاده از این روش وجود دارد.
نتیجهگیری نهایی
از آنجا که شاخص ICC نمیتواند مشخص کند که چقدر از اختلاف در زیرمقیاسها مربوط به خطای اندازهگیری است و همچنین با توجه به تفسیر ساده شاخص انحراف کل، پیشنهاد میشود که پژوهشگران شاخص انحراف کل را در مطالعات پایایی گزارش نمایند.
ملاحظات اخلاقی
پیروی از اصول اخلاق پژوهش
این پژوهش بر گرفته از یک طرح تحقیقاتی است که پروپوزال آن در کمیته اخلاق دانشگاه علوم بهزیستی و توانبخشی مورد تأیید قرار گرفته است (کد: IR.USWR.REC.13960379).
حامی مالی
این پژوهش هیچگونه کمک مالی از سازمانیهای دولتی، خصوصی و غیرانتفاعی دریافت نکرده است.
مشارکت نویسندگان
هر دو نویسنده در آمادهسازی این مقاله مشارکت داشتهاند.
تعارض منافع
نویسندگان اظهار میدارند که این پژوهش هیچ تعارض منافعی ندارد.
References
1.Lin LI. Total deviation index for measuring individual agreement with applications in laboratory performance and bioequivalence. Statistics in Medicine. 2000; 19(2):255-70. [DOI:10.1002/(sici)1097-0258(20000130)19:2<255::aid-sim293>3.0.co;2-8] [PMID]
2.McHorney CA, Ware Jr JE, Rachel Lu JF, Sherbourne CD. The MOS 36-item Short-Form Health Survey (SF-36): III. Tests of data quality, scaling assumptions, and reliability across diverse patient groups. Medical Care. 1994; 32(1):40-66. [DOI:10.1097/00005650-199401000-00004] [PMID]
3.Pan Y, Barnhart HX. Methods for assessing the reliability of quality of life based on SF-36. Statistics in Medicine. 2016; 35(30):5656-65. [DOI:10.1002/sim.7085] [PMID]
4.Montazeri A, Goshtasebi A, Vahdaninia M, Gandek B. The Short Form Health Survey (SF-36): Translation and validation study of the Iranian version. Quality of Life Research. 2005; 14(3):875-82. [DOI:10.1007/s11136-004-1014-5] [PMID]
5.Lin L, Pan Y, Hedayat AS, Barnhart HX, Haber M. A simulation study of nonparametric total deviation index as a measure of agreement based on quantile regression. Journal of Biopharmaceutical Statistics. 2016; 26(5):937-50. [DOI:10.1080/10543406.2015.1094812] [PMID]
ارسال پیام به نویسنده مسئول
| بازنشر اطلاعات | |
 |
این مقاله تحت شرایط Creative Commons Attribution-NonCommercial 4.0 International License قابل بازنشر است. |








